Calculating Loan Amount from Installment and Total Repayment

When building financial applications, loan calculators are a must-have tool. They allow users to see monthly installments, total repayment amounts, interest costs and more. But what if we flip the perspective? Instead of calculating the installment based on the requested loan amount, what if a customer knows how much they want to repay monthly and the total cost they are willing to bear?

Let’s walk through a practical implementation of how to reverse-calculate the loan principal based on:

The monthly installment amount
Total payment amount
Installment term (in months)
Applicable interest rates and fees

This is especially useful for customers planning their budgets strictly around monthly affordability.

📌 Problem Statement

You already have a method that calculates the installment and total repayment based on a requested loan amount:

public CreditCalculationModel CalculateMonthlyAmount(
    double total, int installment, double taxKkdf, double taxBsmv,
    double feeAppraisal, double feeMortgage)

Now, you want to do the reverse:
➡️ Given installment, totalPaymentAmount and fee/tax settings, determine the CreditAmount (i.e. the loan principal).

📊 Required Parameters

To compute this, we need the following:

installment: Loan term in months
totalPaymentAmount: How much the borrower will pay in total
taxKkdf and taxBsmv: Additional financial taxes (percentages)
feeAppraisal and feeMortgage: Fixed fees applied to the loan
Interest and Fee: Configurable values from your credit product

🧠 Understanding the Math

Let’s break down the formula for monthly installment calculation first:

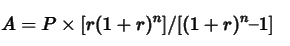
Where:

A = Monthly installment
P = Loan amount
r = Monthly interest rate (adjusted with tax)
n = Number of installments

To reverse the formula, we isolate P:

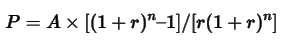
We calculate A from:

monthlyInstallment = (totalPaymentAmount - feeAppraisal - feeMortgage - feePaid) / installment

Where feePaid = CreditAmount * FeeRate

But since CreditAmount is what we want to find, we use iterative estimation (or symbolic isolation) or we approximate by:

CreditAmount = (approximate)

But since our case includes a percentage-based fee, we can refine the logic like this.

🛠️ Implementation in C#

public CreditCalculationModel CalculateLoanAmount(
    int installment, double totalPaymentAmount,
    double taxKkdf, double taxBsmv, 
    double feeAppraisal, double feeMortgage)
{
    // Adjust taxes and fees based on credit type
    var tax = Type == CreditType.HousingCredit ? 0 : taxKkdf + taxBsmv;
    feeAppraisal = Type == CreditType.HousingCredit ? feeAppraisal : 0;
    feeMortgage = Type == CreditType.HousingCredit ? feeMortgage : 0;

    // Monthly interest rate including tax
    var interest = (double)Interest * (1 + (tax / 100)) / 100;

    // Use exponent for the number of installments
    var us = Math.Pow(1 + interest, installment);

    // Estimate the monthly installment (excluding fees)
    var installmentWithoutFees = (totalPaymentAmount - feeAppraisal - feeMortgage) / installment;

    // Reverse-engineer the loan amount
    var creditAmount = installmentWithoutFees * (us - 1) / (interest * us);

    // Compute percentage-based fee
    var feePaid = creditAmount * (double)Fee / 100;

    // Recalculate monthly installment with fees
    var finalMonthlyInstallment = (creditAmount * (interest * us) / (us - 1));

    // Yearly cost rate (effective interest rate)
    var cost = (Math.Pow(1 + interest, 12) - 1) * 100;

    return new CreditCalculationModel
    {
        MonthlyInstallment = finalMonthlyInstallment,
        TotalPaymentAmount = totalPaymentAmount,
        Interest = Interest,
        Fee = feePaid,
        CreditAmount = creditAmount,
        Installment = installment,
        YearlyCostRate = cost
    };
}

✅ Output: What You Get

The method returns a structured CreditCalculationModel:

MonthlyInstallment: Recalculated with real interest
CreditAmount: The estimated loan principal
Fee: Percentage-based fee paid
YearlyCostRate: The effective annual interest rate

📈 Real-World Use Case

This method is perfect for scenarios like:

Mortgage planning: “I want to pay ₺20,000/month for 120 months. How much loan can I get?”
Budget-driven credit advisors
Dynamic loan simulation tools

It provides a customer-centric view of borrowing capacity rather than just system-driven constraints.

🧩 Final Thoughts

Reverse-engineering financial calculations might seem complex at first but with the right formulas and a little math, it becomes a powerful tool in fintech development. By allowing your users to explore scenarios based on total cost and affordability, you empower them with transparency and control, two things modern banking users expect.