Calculating Loan Interest Rate in C# with Precision

📌 Introduction

Calculating a loan's monthly installment is easy with built-in formulas but reversing the problem, figuring out the interest rate based on a known principal, term and monthly payment is a bit trickier.

In this article, we’ll walk through how to calculate the interest rate of a loan using C#, exploring several methods including:

Newton-Raphson iteration
Excel-style financial formulas
.NET alternatives (if available)

By the end, you'll be equipped to embed reliable interest rate calculations into any financial application.

🔢 The Problem

You're given:

creditAmount → The total loan amount
loanTermMonths → The loan duration in months
monthlyPayment → The fixed monthly installment

You want to find:

interestRate → The annual interest rate (%)

Since there's no closed-form algebraic solution, we’ll solve it numerically.

🧠 Understanding the Formula

We base our calculations on the present value of an annuity formula:

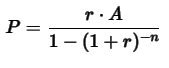
Where:

P is the principal
A is the monthly payment
r is the monthly interest rate
n is the loan term in months

To solve for r, we use iterative methods.

🛠️ Method 1: Newton-Raphson Method

Newton-Raphson is ideal for approximating the root of a real-valued function.

✅ C# Implementation

public static double CalculateInterestRate(double creditAmount, int loanTermMonths, double monthlyPayment)
{
    double guess = 0.05; // Start with 5% annual interest
    double tolerance = 0.00001;
    int maxIterations = 1000;

    for (int i = 0; i < maxIterations; i++)
    {
        double monthlyRate = guess / 12;
        double denominator = 1 - Math.Pow(1 + monthlyRate, -loanTermMonths);

        if (denominator == 0)
            return 0;

        double calculatedPayment = creditAmount * monthlyRate / denominator;
        double error = monthlyPayment - calculatedPayment;

        if (Math.Abs(error) < tolerance)
            return Math.Round(guess * 100, 2); // Annual interest rate as %

        // Derivative approximation
        double derivative = (creditAmount * loanTermMonths * Math.Pow(1 + monthlyRate, -loanTermMonths - 1)) / Math.Pow(denominator, 2);

        guess += error / derivative;
    }

    throw new Exception("Interest rate calculation did not converge.");
}

📊 Method 2: Excel's RATE() Formula (Approximation)

Excel users are familiar with the RATE() function. We can mimic this using numerical libraries or third-party packages like Math.NET.

However, the .NET Framework does not natively include a financial rate solver. You can implement Excel's method using trial-and-error, bisection or Newton-Raphson, as shown.

🧪 Example Use

double creditAmount = 100000;
int loanTermMonths = 24;
double monthlyPayment = 8000;

double interestRate = CalculateInterestRate(creditAmount, loanTermMonths, monthlyPayment);
Console.WriteLine($"Calculated annual interest rate: {interestRate}%");

Expected Output:

Calculated annual interest rate: 4.83%

⚠️ Common Pitfalls

Bad Initial Guesses: Can lead to non-convergence or negative interest rates.
Negative Monthly Payments: Sign errors can throw off results.
Extreme Values: Very short or long terms may require higher precision or iteration limits.

🧹 Optional: Simplified Bisection Method (Stable but Slower)

public static double CalculateInterestRateBisection(double principal, int months, double payment)
{
    double low = 0.0;
    double high = 1.0;
    double mid = 0.0;
    double tolerance = 0.00001;

    while (high - low > tolerance)
    {
        mid = (low + high) / 2;
        double monthlyRate = mid / 12;
        double denominator = 1 - Math.Pow(1 + monthlyRate, -months);
        double guessPayment = principal * monthlyRate / denominator;

        if (guessPayment > payment)
            high = mid;
        else
            low = mid;
    }

    return Math.Round(mid * 100, 2); // Annual rate
}

🧾 Conclusion

Calculating loan interest rates from known values isn't trivial but with the Newton-Raphson method or bisection, we can get accurate results efficiently.

Whether you're building a loan calculator, financial dashboard or simulation tool, this technique is a valuable addition to your backend arsenal.